ÚLTIMO TEMA: LA DISTRIBUCIÓN DE PROBABILIDAD CONTINUA, LA DISTRIBUCIÓN NORMAL N( 0, 1)

Una variable aleatoria continua, X, sigue una distribución normal de media μ y desviación típica σ, y se designa por N(μ, σ), si se cumplen las siguientes condiciones:

1. La variable puede tomar cualquier valor: (-∞, +∞)

2. La función de densidad, es la expresión en términos de ecuación matemática de la curva de Gauss:

Esta función, de difícil expresión algebraica,
tiene una gráfica característica, llamada comúnmente
CAMPANA DE GAUSS y tiene las siguientes características:

El campo de existencia es cualquier valor real, es decir, (-∞, +∞).

Es simétrica respecto a la media µ.

Tiene un máximo en la media µ.

Crece hasta la media µ y decrece a partir de ella.

En los puntos µ − σ y µ + σ presenta puntos de inflexión.

El eje de abscisas es una asíntota de la curva.

El área del recinto determinado por la función y el eje de abscisas es igual a la unidad.

Como toda distribución de probabilidad continua, NO PERMITE CALCULAR probabilidades de valores concretos, sino la probabilidad de intervalos entre dos valores cualquiera de la variable.

Por suerte, el cálculo de probabilidades es fácil y accesible ya que está tabulada. Es decir, las probabilidades se calculan a partir de una tabla de valores de una distribución de media 0 y de desviación típica 1. También se llama N(0, 1). 

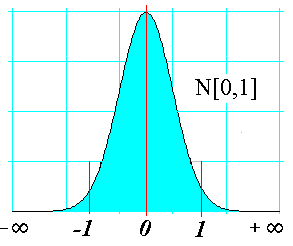
La tabla mide la probabilidad desde -∞ hasta un valor k, es decir mide p(z≤ k), que es la tabla que tenéis en el cuadernillo. Con esta tabla y conociendo las propiedades de la probabilidad podemos calcular cualquier caso

p(z =a) =  0

p(z≤ a) = f(a) ---> se mira directamente en la tabla

p(a < z ≤ b) = f(b) - f(a)

p(z> a) = 1 - p(z≤ a) = 1 - f(a)

Esta tabla tiene además el inconveniente de que no puedes encontrar probabilidades para valores de z negativos, pero al ser una función simétrica podemos hacer los cálculos de la siguiente manera

p(z≤ -a) = p(z> a) = 1 - p(z≤ a) = 1 - f(a)

p(z> -a) = p(z≤ a) = f(a)

Os pongo el enlace a una página para practicar, AQUÍ

REPASOS DE PROBABILIDAD Y DISTRIBUCIÓN BINOMIAL

Hola, os pongo los enlaces a páginas web con ejercicios de probabilidad para practicar en casa y para repasar. Todos los ejercicios tienen su solución.

Repaso de probabilidad

Ejercicios de probabilidad (pdf a partir de página 438)

Repaso de distribución binomial (pdf a partir de página 474)

Recordad que en el examen no voy a poner ejercicios complicados

DISTRIBUCIÓN DE PROBABILIDAD DISCRETA: DISTRIBUCIÓN BINOMIAL

Hola, hoy hemos empezado el penúltimo tema del curso. La distribución binomial. Esta se caracteriza por una serie n de experimentos independientes, que puede tomar dos posibilidades:
Éxito: con una probabilidad constante p
Fracaso: con una probabilidad también constante (1 -p) también llamada q

El cálculo de probabilidades de x éxitos y por tanto (n -x) fracasos independientemente del orden en que se produzcan los éxitos o fracasos se puede calcular con la siguiente fórmula o función


Dicho esto, cuando un experimento aleatorio sigue una distribución binomial, lo abreviamos con los datos siguientes B(n, p)

El cálculo de los parámetros representativos se calcula muy fácilmente a partir de lo escrito anteriormente.
Media = n·p
Desviación típica = raíz cuadrada de  n·p·(1-p)

Os dejo con un enlace a problemas típicos de distribución binomial AQUÍ

CÁLCULO DE PROBABILIDADES A POSTERIORI. TEOREMA DE BAYES

Hola, os pongo un vídeo con un ejercicio resuelto paso a paso para cálculo de probabilidades a posteriori. La distinción entre cálculo de probabilidades a priori y a posteriori, es que mientras a priori calculamos las probabilidades sabiendo las condiciones de antemano, en las probabilidades a posteriori es que conociendo el resultado final de lo que ha ocurrido podamos calcular la probabilidad de que se haya originado al principio de una manera u otras.

Como dicen en el video no hace falta saber aplicar el teorema de Bayes, pues su formulación es muy complicada, sino saber aplicar una probabilidad condicionada. También se puede resolver con una tabla de contingencia como veréis aquí abajo si os traduzco el ejemplo a una tabla

	Urna 1	Urna 2	Total
Roja	½ · 2/6= 1/6	½ · 3/5= 3/10	7/15
Amarilla	½ · 4/6=2/6	½ · 2/5= 1/5	8/15
Total	1/2	1/2	1

Nos quedamos con la fila de la condición que se ha cumplido, es decir, que ha sucedido bola roja, y dividimos la casilla de la urna 1 con el total de sacar roja.

P(urna₁ / R) = 1/6 : 7/15 = 5/14

ESTADÍSTICAS BIDIMENSIONALES CON HOJA DE CÁLCULO

Hola, como hemos visto en clase, cuando manejamos datos de 2 magnitudes distintas, si queremos ver si existe alguna relación entre ambas magnitudes hacemos una regresión lineal, o sea, construimos sobre la nube de puntos (x, y) con los datos recogidos una recta que intente dejar tantos puntos por encima como por debajo y de forma también que la distancia de dichos puntos a la recta sea la menor posible.


Hemos visto que el parámetro que mejor cuantifica esta correlación lineal es el coeficiente de correlación (r) de Pearson, que puede variar entre -1 y 1. El signo +/- nos indica si la correlación es directa/inversa respectivamente. Y el valor numérico tiene que ser lo más cercano a 1, para decidir si la relación entre variables es más fiable.

Grados de correlación:
1 --> relación funcional (los datos siguen la ecuación de la recta de regresión)
>0.9 --> correlación muy fuerte
0.7-0.9 --> correlación fuerte
0.6-0.7 --> correlación moderada
0.5-0.6 --> correlación débil
por debajo de 0.5 decimos que la correlación es muy débil, los datos de ambas magnitudes no guardan relación a la vista de los datos observados.

Obtener la recta de regresión es muy fácil con medios tecnológicos (ordenadores y calculadoras científicas).  En resumen, muchos ejercicios de correlación entre variables se pueden resolver fácilmente con una hoja de cálculo como Excel.

INSTRUCCIONES
1. Copiar en columnas los datos de los que hacer la correlación. Marcar con el ratón
2. menú insertar gráfico de dispersión de puntos x - y
3. menú de diseño, agregar elemento de gráfico y elegir línea de tendencia ---> lineal
4. menú de diseño, agregar elemento de gráfico,  más opciones ---> presentar ecuación en el gráfico
5. para hallar coeficiente de correlación r ----> menú fórmulas, elegir  más funciones       ---> estadísticas y buscar coef.de.correl. marcamos las columnas de x en la matriz 1, marcamos las columnas de y en la matriz 2 y aceptar. Una variante más sencilla es a partir del punto 4, además de presentar ecuación en el gráfico, marcamos presentar el valor R cuadrado. r es la raíz cuadrada del valor presentado en el gráfico. El signo +/- es el mismo que el del coeficiente de x en la recta de regresión.

El trabajo que os he encargado es buscar datos estadísticos en  www.ine.es, o de Murcia en econet.carm.es, referidos a datos económico sociales y relacionarlos con otros datos referidos a condiciones sanitarias, servicios, etc... para que comprobéis la relación entre variables, el grado de relación r, y la recta de regresión.  Espero que me sorprendáis. Guardáis las hojas de cálculo con vuestro nombre y apellidos, en cada hoja se deben ver las gráficas, la recta de regresión y r,  y las  conclusiones,  y las mandáis al siguiente e-mail: matesinstitutolamanga@gmail.com
Fecha límite de entrega de trabajos: 25 de abril de 2017 a las 23:59 h

TASA DE VARIACIÓN INSTANTÁNEA: DERIVADA DE LA FUNCIÓN EN UN PUNTO

Como veremos más adelante, la tasa de variación instantánea es la tasa de variación media aplicada a puntos tan cercanos como un punto a sí mismo. La solución de ese límite es una indeterminación 0/0 cuya resolución lleva a valores determinados. A este proceso le llamamos hallar la derivada de la función en un punto x = a

En resumen, TVI (en x =a) es hallar la derivada de la función en x =a  ó f'(a)

Luego veremos que es más fácil hallar la función derivada mediante reglas de derivación y sustituir la variable por un número y operar.

TASA DE VARIACIÓN MEDIA. EJERCICIOS

Como ya vimos en clase la tasa de variación media, os pongo ejercicios de tasas de  variación media.

Pinchad AQUÍ

CÁLCULO DE LÍMITES Y RESOLUCIÓN DE INDETERMINACIONES

En esta página encontraréis ejemplos para practicar los límites de funciones, teniendo en cuenta las indeterminaciones que surgen y explicando la solución paso a paso.

INTERPOLACIÓN POLINÓMICA

La interpolación polinómica consiste en hallar la expresión algebraica de una función sabiendo  coordenadas de puntos por donde pasa. En este caso la función es un polinomio, y en vuestro nivel sólo vamos a ver hasta la interpolación polinómica.
Nota previa: para un polinomio de grado n, necesitamos (n + 1) coordenadas. En nuestro caso,
para polinomios de grado 0, necesitamos 1 coordenada,
para polinomios de grado 1, necesitamos 2 coordenadas (2 puntos para trazar la recta)
para polinomios de grado 2, necesitamos 3 coordenadas (3 puntos para trazar la parábola)

Método: mediante sistema de ecuaciones lineales. En la fórmula general de cada polinomio y = P(x), sustituimos y por la coordenada y de cada punto, la x por la coordenada x de cada punto y resolvemos los sistemas resultantes,

gráficas de funciones con excel

Hola a todos, os pongo una hoja de cálculo Excel que os servirá para las matemáticas de este curso. Para descargar el archivo pinchad AQUÍ.